PSMPC – Pulse-step model predictive controller

Block SymbolLicensing group: ADVANCED

Function Description
The PSMPC block can be used for control of hardly controllable linear time-invariant systems with manipulated value constraints (e.g. time delay or non-minimum phase systems). It is especially well suited for the case when fast transition without overshoot from one level of controlled variable to another is required. In general, the PSMPC block can be used where the PID controllers are commonly used.

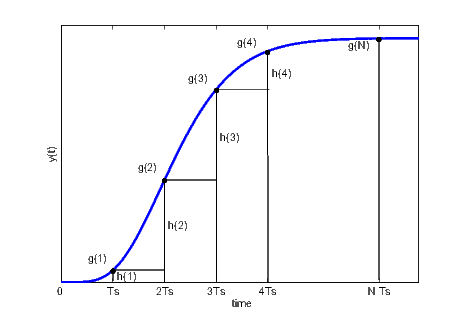
The PSMPC block is a predictive controller with explicitly defined constraints on the amplitude of manipulated variable.

The prediction is based on the discrete step response $g\left(j\right),j=1,\dots ,N$ is used. The figure above shows how to obtain the discrete step response $g\left(j\right),j=0,1,\dots ,N$ and the discrete impulse response $h\left(j\right),j=0,1,\dots ,N$ with sampling period $T_S$ from continuous step response. Note that $N$ must be chosen such that $N\cdot T_S>t_{95}$, where $t_{95}$ is the time to reach 95 % of the final steady state value.

For stable, linear and t-invariant systems with monotonous step response it is also possible to use the moment model set approach [4] and describe the system by only 3 characteristic numbers $\kappa$, $\mu$, and ${\sigma }^2$, which can be obtained easily from a very short and simple experiment. The controlled system can be approximated by first order plus dead-time system

or second order plus dead-time system

with the same characteristic numbers. The type of approximation is selected by the imtype parameter.

To lower the computational burden of the open-loop optimization, the family of admissible control sequences contains only sequences in the so-called pulse-step shape depicted below:

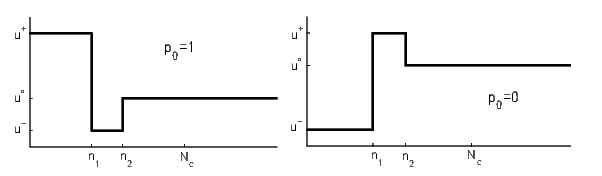
Note that each of these sequences is uniquely defined by only four numbers $n_1,n_2\in \left\{0,\dots ,N_C\right\}$, $p_0$ and , where $N_C\in \left\{0,1,\dots \right\}$ is the control horizon and $u^{-},u^{+}$ stand for the given lower and upper limit of the manipulated variable. The on-line optimization (with respect to $p_0$, $n_1$, $n_2$ and $u^{\infty }$) minimizes the criterion

where $ê\left(k+i|k\right)$ is the predicted control error at time $k$ over the coincidence interval $i\in \left\{N_1,N_2\right\}$, $\Delta û\left(k+i|k\right)$ are the differences of the control signal over the interval $i\in \left\{0,N_C\right\}$ and $\lambda$ penalizes the changes in the control signal. The algorithm used for solving the optimization task (7.3) combines brute force and the least squares method. The value $u^{\infty }$ is determined using the least squares method for all admissible combinations of $p_0$, $n_1$ and $n_2$ and the optimal control sequence is selected afterwards. The selected sequence in the pulse-step shape is optimal in the open-loop sense. To convert from open-loop to closed-loop control strategy, only the first element of the computed control sequence is applied and the whole optimization procedure is repeated in the next sampling instant.

The parameters $N_1$, $N_2$, $H_C$, and $\lambda$ in the criterion (7.3) take the role of design parameters. Only the last parameter $\lambda$ is meant for manual tuning of the controller. In the case the model in the form (7.1) or (7.2) is used, the parameters $N_1$ and $N_2$ are determined automatically with respect to the $\mu$ and ${\sigma }^2$ characteristic numbers. The controller can be then effectively tuned by adjusting the characteristic numbers $\kappa$, $\mu$ and ${\sigma }^2$.

Warning
It is necessary to set the sr array sufficiently large to avoid Matlab/Simulink crash when using the PSMPC block for simulation purposes. Especially when using FOPDT or SOPDT model, the sr array size must be greater than the length of the internally computed discrete step response.

2023 © REX Controls s.r.o., www.rexygen.com