PSMPC – Prediktivní „pulse-step“ regulátor

Symbol blokuPotřebná licence: ADVANCED

Popis funkce
Funkční blok PSMPC (Pulse Step Model Predictive Control) je určen pro realizaci vysoce kvalitních regulátorů pro obtížně regulovatelné lineární časově invariantní soustavy s omezením akční veličiny (např. soustavy s dopravním zpožděním nebo s neminimální fází). Zvlášť výhodný je pro případy, kdy je požadován velmi rychlý přechod z jedné hodnoty regulované veličiny na druhou bez překmitu. Regulátor PSMPC však může být obecně použit všude tam, kde je běžně nasazován standardní PID regulátor a kde žádáme vysokou kvalitu regulace.

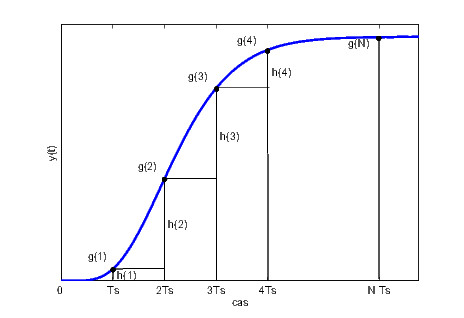
PSMPC je prediktivní regulátor s explicitně zadaným intervalovým omezením akční veličiny. Pro účely predikce je použit model ve tvaru diskrétní přechodové charakteristiky $g (j), j = 1, . . ., N$ . Na obrázku výše je naznačen způsob, jakým lze tuto posloupnost získat ze spojité přechodové charakteristiky. Poznamenejme, že $N$ musí být zvoleno dostatečně velké, aby přechodová charakteristika byla popsána až do ustáleného stavu ( $N T_{S} > t_{95}$ , kde $T_{S}$ je perioda vzorkování regulátoru a $t_{95}$ je doba ustálení na 95 % konečné hodnoty). Pro systémy s monotónní přechodovou charakteristikou je alternativně možné použít momentový množinový model [3] a popsat systém pouze třemi charakteristickými čísly $κ, μ$ a $σ^{2}$ , které je možno určit z jednoduchého pulzního experimentu. Řízený systém pak aproximujeme buď přenosem prvého řádu s dopravním zpožděním

F_{F O P D T} (s) = \frac{K}{τ s + 1} \cdot e^{- D s}, κ = K, μ = τ + D, σ^{2} = τ^{2}

(7.1)

nebo přenosem druhého řádu s dopravním zpožděním

F_{S O P D T} (s) = \frac{K}{{(τ s + 1)}^{2}} \cdot e^{- D s}, κ = K, μ = 2 τ + D, σ^{2} = 2 τ^{2}

(7.2)

se stejnými charakteristickými čísly. Typ aproximace se zadává parametrem imtype.

Pro zjednodušení on-line optimalizace v otevřené smyčce je množina přípustných posloupností řízení omezena pouze na posloupnosti ve tvaru "pulz-skok"zobrazené na obrázku níže.

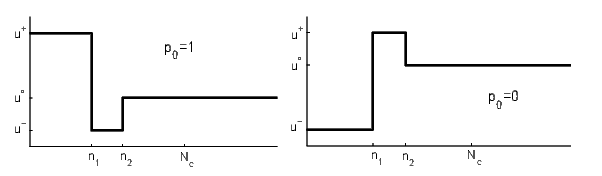
Poznamenejme, že každá taková posloupnost je jednoznačně určena jen třemi čísly $n_{1}, n_{2} \in \{0, \dots, N_{C}\}$ a $u^{\infty} \in <u^{-}, u^{+}>$ , kde $N_{C} \in \{0, 1, \dots\}$ je horizont řízení a $u^{-}, u^{+}$ označují po řadě zadanou dolní a horní mez akční veličiny regulátoru. On-line optimalizace (vzhledem k $n_{1}, n_{2}$ a $u^{\infty}$ ) spočívá v minimalizaci kritéria

I = \sum_{i = N_{1}}^{N_{2}} ê {(k + i | k)}^{2} + λ \sum_{i = 0}^{N_{C}} Δ û {(k + i |k)}^{2} \to min,

(7.3)

kde $ê (k + i | k)$ je v kroku $k$ predikovaná regulační odchylka na intervalu predikce $i \in \{N_{1}, N_{2}\}$ , $Δ û (k + i | k)$ jsou diference řídicího signálu na intervalu $i \in \{0, N_{C}\}$ a $λ$ je koeficient penalizace změn akční veličiny. Pro nalezení optima úlohy (7.3) je použita kombinace metody nejmenších čtverců a hrubé síly. Hodnota $u^{\infty}$ je určena pro všechny přípustné kombinace $p_{0}$ , $n_{1}$ a $n_{2}$ a následně je z nich vybrána optimální řídicí sekvence pro řízení v otevřené smyčce. Ve skutečnosti je však vždy aplikován pouze prvý krok této řídicí sekvence a v další vzorkovací periodě je celý optimalizační proces zopakován. Tím se řídicí strategie mění na zpětnovazební řízení.

Parametry prediktivního regulátoru, kromě modelu řízené soustavy a omezení jejího vstupu, jsou horizont řízení $N_{C}$ , horizont predikce $N_{1}, N_{2}$ a koeficient $λ$ . Pouze poslední uvedený parametr je určen pro ruční doladění kvality regulace při rutinním uvádění do provozu. V případě použití modelu soustavy ve tvaru přenosu (7.1) nebo (7.2) jsou parametry $N_{1}, N_{2}$ zvoleny automaticky na základě charakteristických čísel $μ, σ^{2}$ . Regulátor potom může být efektivně laděn „ručně“ pouze seřizováním charakteristických čísel procesu $κ, μ, σ^{2}$ .

Varování
Při použití bloku PSMPC pro simulaci v systému Matlab/Simulink je třeba zajistit, aby parametr nsr byl dostatečně velký, tak aby jím definovaný buffer pojmul interně vygenerovanou přechodovou charakteristiku určenou z FOPDT nebo SOPDT modelu. V opačném případě dojde k havárii systému Matlab/Simulink.

Vstupy

sp	Požadovaná hodnota (setpoint)	Double (F64)
pv	Řízená veličina	Double (F64)
tv	Veličina pro vysledování (použitý řídicí signál)	Double (F64)
hv	Hodnota výstupu v manuálním režimu	Double (F64)
MAN	Manuální nebo automatický režim	Bool
	off .. automatický režim on ... manuální režim

Výstupy

mv	Akční zásah regulátoru (manipulated variable)	Double (F64)
dmv	Rychlostní výstup regulátoru (diference)	Double (F64)
de	Regulační odchylka	Double (F64)
SAT	Saturace	Bool
	off .. lineární zákon řízení on ... výstup regulátoru je saturován
pve	Predikovaná hodnota regulované veličiny na základě zadaného modelu	Double (F64)
iE	Kód chyby	Long (I32)
	0 .... bez chyby 1 .... nesprávný FOPDT model 2 .... nesprávný SOPDT model 3 .... chyba v zadání přechodové charakteristiky

Parametry

nc	Délka horizontu řízení ( $N_{C}$ ) $⊙$ 5	Long (I32)
np1	Začátek koincidenčního intervalu ( $N_{1}$ ) $⊙$ 1	Long (I32)
np2	Konec koincidenčního intervalu ( $N_{2}$ ) $⊙$ 10	Long (I32)
lambda	Koeficient penalizace změn řízení ( $λ$ ) $⊙$ 0.05	Double (F64)
umax	Horní mez akčního zásahu regulátoru ( $u^{+}$ ) $⊙$ 1.0	Double (F64)
umin	Dolní mez akčního zásahu regulátoru ( $u^{-}$ ) $⊙$ -1.0	Double (F64)
imtype	Typ modelu řízené soustavy $⊙$ 3	Long (I32)
	1 .... model prvního řádu 2 .... model druhého řádu 3 .... přechodová charakteristika
kappa	Statické zesílení ( $κ$ ) $⊙$ 1.0	Double (F64)
mu	Míra zpoždění soustavy ( $μ$ ) $⊙$ 20.0	Double (F64)
sigma	Míra délky odezvy soustavy ( $\sqrt{σ^{2}}$ ) $⊙$ 10.0	Double (F64)
nsr	Délka diskrétní přechodové charakteristiky ( $N$ ), pozor na varování uvedené výše $↓$ 10 $↑$ 10000000 $⊙$ 11	Long (I32)
sr	Diskrétní přechodová charakteristika ( $[g (1), \dots, g (N)]$ ) $⊙$ [0 0.2642 0.5940 0.8009 0.9084 0.9596 0.9826 0.9927 0.9970 0.9988 0.9995]	Double (F64)

[Předchozí] [Na začátek] [Výše] [Další]