SMHCC – Sliding mode heating/cooling controller

Block SymbolLicensing group: ADVANCED

Function Description
The sliding mode heating/cooling controller SMHCC is a novel high quality control algorithm intended for temperature control of heating-cooling (possibly asymmetrical) processes with ON-OFF heaters and/or ON-OFF coolers. The plastic extruder is a typical example of such process. However, it can also be applied to many similar cases, for example in thermal systems where a conventional thermostat is employed. To provide the proper control function the block SMHCC must be combined with the block PWM (Pulse Width Modulation) as depicted in the following figure.

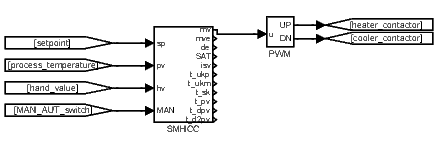
It is important to note that the block SMHCC works with two time periods. The first period $T_S$ is the sampling time of the process temperature, and this period is equal to the period with which the block SMHCC itself is executed. The second period $T_C=i_{pwmc}{T}_S$ is the control period with which the block SMHCC generates manipulated variable. This period $T_C$ is also equal to the cycle time of PWM block. At every instant when the manipulated variable mv is changed by SMHCC the PWM algorithm recalculates the width of the output pulse and starts a new PWM cycle. The time resolution $T_R$ of the PWM block is third time period involved with. This period is equal to the period with which the block PWM is run and generally may be different from $T_S$. To achieve the high quality of control it is recommended to choose $T_S$ as minimal as possible ($i_{pwmc}$ as maximal as possible), the ratio $T_C∕T_S$ as maximal as possible but $T_C$ should be sufficiently small with respect to the process dynamics. An example of reasonable values for an extruder temperature control is as follows:

The control law of the block SMHCC in automatic mode ($\mathtt{\text{MAN}}=\mathtt{\text{off}}$) is based on the discrete dynamic sliding mode control technique and special 3rd order filters for estimation of the first and second derivatives of the control error.

The first control stage, after a setpoint change or upset, is the reaching phase when the dynamic sliding variable

is forced to zero. In the above definition of the sliding variable, $e_k,{ė}_k,{ë}_k$ denote the filtered deviation error $\left(\mathtt{\text{pv}}-\mathtt{\text{sp}}\right)$ and its first and second derivatives in the control period $k$, respectively, and $\xi ,\Omega$ are the control parameters described below. In the second phase, $s_k$ is hold at the zero value (the sliding phase) by the proper control "bangs". Here, the heating action is alternated by cooling action and vice versa rapidly. The amplitudes of control actions are adapted appropriately to guarantee $s_k=0$ approximately. Thus, the hypothetical continuous dynamic sliding variable

is approximately equal to zero at any time. Therefore the control deviation behaves according to the second order differential equation

describing so called zero sliding dynamics. From it follows that the evolution of $e$ can be prescribed by the parameters $\xi ,\Omega$. For stable behavior, it must hold $\xi >0,\Omega >0$. A typical optimal value of $\xi$ ranges in the interval $\left[4,8\right]$ and $\xi$ about $6$ is often a satisfactory value. The optimal value of $\Omega$ strongly depends on the controlled process. The slower processes the lower optimal $\Omega$. The recommended value of $\Omega$ for start of tuning is $\pi ∕\left(5T_C\right)$.
The manipulated variable mv usually ranges in the interval $\left[-1,1\right]$. The positive (negative) value corresponds to heating (cooling). For example, $\mathtt{\text{mv}}=1$ means the full heating. The limits of mv can be reduced when needed by the controller parameters hilim_p and hilim_m. This reduction is probably necessary when the asymmetry between heating and cooling is significant. For example, if in the working zone the cooling is much more aggressive than heating, then these parameters should be set as $\mathtt{\text{hilim\_p}}=1$ and $\mathtt{\text{hilim\_m}}<1$. If we want to apply such limitation only in some time interval after a change of setpoint (during the transient response) then it is necessary to set initial value of the heating (cooling) action amplitude u0_p (u0_m) to the suitable value less than hilim_p (hilim_m). Otherwise set $\mathtt{\text{u0\_p}}=\mathtt{\text{hilim\_p}}$ and $\mathtt{\text{u0\_m}}=\mathtt{\text{hilim\_m}}$.

The current amplitudes of heating and cooling uk_p, uk_m, respectively, are automatically adapted by the special algorithm to achieve so called quasi sliding mode, where the sign of $s_k$ alternately changes its value. In such a case the controller output isv alternates the values $1$ and $-1$. The rate of adaptation of the heating (cooling) amplitude is given by the time constant taup (taum). Both of these time constants have to be sufficiently high to provide the proper function of adaptation but the fine tuning is not necessary. Note for completeness that the manipulated variable mv is determined from the action amplitudes uk_p, uk_m by the following expression

Further, it is important to note that quasi sliding is seldom achievable because of a process dead time or disturbances. The suitable indicator of the quality of sliding is again the output isv. If the extraordinary fine tuning is required then it may be tried to find the better value for the bandwidth parameter beta of derivative filter, otherwise the default value $0.1$ is preferred. In the manual mode ($\mathtt{\text{MAN}}=\mathtt{\text{on}}$) the controller input hv is (after limitation to the range $\left[-\mathtt{\text{hilim\_m}},\mathtt{\text{hilim\_p}}\right]$) copied to the manipulated variable mv.

2020 © REX Controls s.r.o., www.rexygen.com